Ap Calculus Piecewise Continuously Differentiable Function

All AP Calculus AB Resources

Wolframalpha--plot_piecewisexxlt03-x0ltxlt213-xxgt2--2013-09-10_1008

is differentiable for which of the following values of ?

Correct answer:

f'(x) Correct graph

Consider the graph of above. What can we say about when x = 0 ?

Possible Answers:

f(x) has a horizontal tangent at x = 0 .

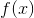
Two or more of these are correct.

None of these are correct.

f(x) has a removable discontinuity at x = 0 .

f(x) is discontinuous at x = 0 because there is a sharp turn at f'(0) .

Correct answer:

f(x) has a horizontal tangent at x = 0 .

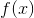
Explanation:

Note that f'(0) = 0 , indicating that there is a horizontal tangent on f(x) at x = 0 . More specifically, the derivative is the slope of the tangent line. If the slope of the tangent line is 0, then the tangent is horizontal.

The other two are incorrect because sharp turns only apply when we want to take the derivative of something. The derivative of a function at a sharp turn is undefined, meaning the graph of the derivative will be discontinuous at the sharp turn. (To see why, ask yourself if the slope at x = 0 is positive 1 or negative 1?) On the other hand, integration is less picky than differentiation: We do not need a smooth function to take an integral.

In this case, to get from f'(x) to f(x) , we took an integral, so it didn't matter that there was a sharp turn at the specified point. Thus, neither function had any discontinuities.

Is the following piecewise function continuous for all? If not, state where it is discontinuous.

$f(x) = \left{\begin{Bmatrix} x^2+3 & 3 < x \\ 5x-3 & 3 \leq x < 5 \\ 11(x-3) &x \geq 5 \\ \end{matrix}\right.}$

Possible Answers:

No. The function is not continuous at x = 5 .

Yes. The function is continuous at all.

No. The function is not continuous at both x = 3 and x = 5 .

No. There are sharp turns at x = 3 and x = 5 .

No. The function is not continuous at x = 3 .

Correct answer:

Yes. The function is continuous at all.

Explanation:

To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.

At x =3 , this means checking that x^2 + 3 and 5x -3 have the same value. More formally, we are checking to see that $f(3) = \lim_{x\rightarrow3^-} f(x)$ , as to be continuous at a point, a function's left and right limits must both equal the function value at that point.

Plugging 3 into both, we see that both of them are 12 at x =3 . Thus, they meet up smoothly.

Next, for x = 5 , we have 5x -3 and 11(x-3) . Plugging in 5, we get 22 for both equations.

As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.

Note, therearesharp turns at x = 3 and x = 5 , but this only means the function isn't differentiable at these points -- we're only concerned with continuity, which is if the equations meet up. Thus, the function is continuous.

At x=6 the funciton described above is:

Possible Answers:

continuous but not differentiable

both continuous and diffentiable

undefined

neither differentiable or continuous

differentiable but not continuous

Correct answer:

both continuous and diffentiable

Explanation:

The answer is both.

If graphed the student will see that the two graphs are continuous at x=6 . There is no gap in the graph or no uneven transitions. If the graph is continuous then it is differentiable so it must be both.

Which of the following functions contains a removeable discontinuity?

Correct answer:

$f(x)=\frac{1+x^{3}}{1+x}$

Explanation:

A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at x=a , then the limit as approaches exists, but the value of f(a) does not.

For example, the function $f(x)=\frac{1+x^3}{1+x}$ contains a removeable discontinuity at x=-1 . Notice that we could simplify f(x) as follows:

$f(x)=\frac{1+x^3}{1+x}=\frac{(1+x)(x^2-x+1)}{1+x}=x^{2}-x+1$ , where $x\neq -1$ .

Thus, we could say that $\lim_{x\rightarrow -1}\frac{1+x^3}{1+x}=\lim_{x\rightarrow -1}x^2-x+1=(-1)^2-(-1)+1=3$ .

As we can see, the limit of f(x) exists at x=-1 , even though f(-1) is undefined.

What this means is that f(x) will look just like the parabola with the equation $x^{2}-x+1$ EXCEPT when x=-1 , where there will be a hole in the graph. However, if we were to just define f(-1)=3 , then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at x=-1 .

The functions

$f(x)=\frac{x}{1-x^{2}}$ , and

$f(x)=1-(\ln x)^{2}$

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.

The functions

$f(x)=x^{2}\sin x^{2}$ and $f(x)=\frac{x+1}{1+x^{2}}$ are continuous over all the real values of ; they have no discontinuities of any kind.

The answer is

$f(x)=\frac{1+x^{3}}{1+x}$ .

If $\lim_{x \to 0} f(x)$ exists,

Possible Answers:

$\lim_{x \to \infty} f(x)$ exists.

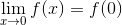
f(0) exists and $\lim_{x \to 0}f(x) = f(0)$

f(x) must be continuous at x=0 .

f(x) must be continuous at all values.

We cannot conclude any of the other answers.

Correct answer:

We cannot conclude any of the other answers.

Explanation:

Unless we are explicitly told so, via graph, information, or otherwise, we cannot assume f(x) is continuous at x=0 unless $\lim_{x \to 0}f(x) = f(0)$ , which is required for f(x) to be continuous at x=0 .

We cannot assume anything about the existence of $\lim_{x \to \infty} f(x)$ , because we do not know what f(x) is, or its end behavior.

$f(x) = \left\{\begin{matrix} x^{2}- 3x+ 17,& x<2 \\ 17, & x=2\\ x^{2}- 4x+ 16,&x > 2 \end{matrix}\right.$

Which of the following is equal to $\lim_{x\rightarrow 2 }f(x)$ ?

Correct answer:

$\lim_{x\rightarrow 2 }f(x)$ does not exist.

Explanation:

The limit of a function as approaches a value $x_{0}$ exists if and only if the limit from the left is equal to the limit from the right; the actual value of $f(x_{0})$ is irrelevant. Since the function is piecewise-defined, we can determine whether these limits are equal by finding the limits of the individual expressions. These are both polynomials, so the limits can be calculated using straightforward substitution:

$\lim_{x\rightarrow 2^{-} }f(x)= \lim_{x\rightarrow 2^{-} } (x^{2}- 3x+ 17) = 2^{2}- 3(2)+ 17 = 15$

$\lim_{x\rightarrow 2^{+} }f(x) = \lim_{x\rightarrow 2^{+} }(x^{2}- 4x+ 16) = 2^{2}- 4(2)+16 = 12$

$\lim_{x\rightarrow 2 }f(x)$ does not exist, because $\lim_{x\rightarrow 2^{-} }f(x) \ne \lim_{x\rightarrow 2^{+} }f(x)$ .

Determine any points of discontinuity for the function:

$f(x)=\frac{2}{ln(x^2)}$

Correct answer:

x=-1,1

Explanation:

For a function to be continuous the following criteria must be met:

The function must exist at the point (no division by zero, asymptotic behavior, negative logs, or negative radicals).
The limit must exist.
The point must equal the limit. (Symbolically, $\lim_{x\rightarrow c}f(x)=f(c)$ ).

It is easiest to first find any points where the function is undefined. Since our function involves a fraction and a natural log, we must find all points in the domain such that the natural log is less than or equal to zero, or points where the denominator is equal to zero.

To find the values that cause the natural log to be negative we set

ln(x^2)=0

$e^{ln(x^2)}=e^{0}$

x^2=1

$x=\pm1$

Therefore, those x values will yield our points of discontinuity. Normally, we would find values where the natural log is negative; however, for all x^2 the function is positive.

All AP Calculus AB Resources

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice ("Infringement Notice") containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys' fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner's agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

daileyderessamble.blogspot.com

Source: https://www.varsitytutors.com/ap_calculus_ab-help/functions-graphs-and-limits/continunity-as-a-property-of-functions

Ap Calculus Piecewise Continuously Differentiable Function

All AP Calculus AB Resources

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

0 Response to "Ap Calculus Piecewise Continuously Differentiable Function"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel